【LeetCode 日记】面试题46. 把数字翻译成字符串

​

原题地址： https://leetcode-cn.com/problems/ba-shu-zi-fan-yi-cheng-zi-fu-chuan-lcof

题目描述

给定一个数字，我们按照如下规则把它翻译为字符串：0 翻译成 “a” ，1 翻译成 “b”，……，11 翻译成 “l”，……，25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数，用来计算一个数字有多少种不同的翻译方法。

示例 1:

输入: 12258
输出: 5
解释: 12258 有 5 种不同的翻译，分别是”bccfi”, “bwfi”, “bczi”, “mcfi”和”mzi”

提示：

0 <= num < 231

思路

我们另 f(n)表示给定数字 num 的情况下，从 num 的第 1 位（包含）到第 n 位（包含）有多少种不同的翻译方法。

我们从几个简单的例子入手，尝试打开思路。

对于数字 12258 来说:

| （挡板）表示从这里分开翻译， ，（逗号）表示分割多个翻译方式。

• f(1) = 1，分别为 1。
• f(2) = 2，分别为 1|2， 12。
• f(3) = 3，分别为 1|2|2，1|22，12|2
• …

其实对于 f(3) 来说， 我手动的情况下，是这么想的：

• 先把 f(2) 结果搬过来，即 1|2，12
• 在 f(2)的基础上分割，我要添加第三位，也就是一个 2 到末尾。 1|2|2 这样是行的， 12|2 同样是可以的。
• 继续在 f(1) 的基础上分割，我要添加第三位，也就是一个 2 到末尾。 1|22

那么总的情况就是三种。OK，总结下我的逻辑：

• 如果我不可以和前面的数字组成 10 - 25 之间的数，那么在 f(n - 1) 的末尾添加挡板
• 如果可以，同时在 f(n - 1)和 f(n -2) 的末尾添加挡板

用图来表示：

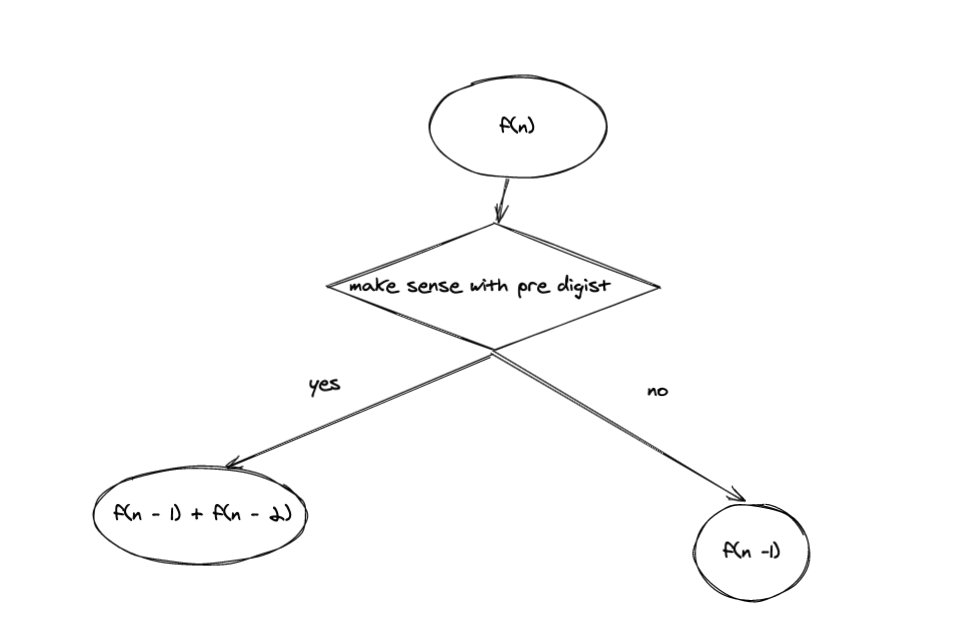
因此，实际上这道题就是爬楼梯的换皮题。

代码

class Solution:
    def translateNum(self, num: int) -> int:
        @lru_cache
        def helper(s: str) -> int:
            if not s: return 1
            pre = helper(s[:-1])
            if 10 <= int(s[-2:]) <= 25:
                return pre + helper(s[:-2])
            return pre
        return helper(str(num))

复杂度分析

• 时间复杂度：最坏的情况，每一个数组都可以和前面的组成新的数组， 有大约 $2^N$ 种组合，因此时间复杂度为 $O(2^N)$，而我这里使用了 @lru_cache 因此不会有重复计算，时间复杂度为 $(N)$，其中 N 为 数字长度。
• 空间复杂度：由于空间复杂的受递归调用栈的影响，因此空间复杂度为 $O(2^N)$，而我这里使用了 @lru_cache 因此不会有重复计算，空间复杂度为 $(N)$，其中 N 为 数字长度。

如果你愿意的话，其实优化起来也比较简单，我们只需要 bottom-up 即可。

class Solution:
    def translateNum(self, num: int) -> int:
        s = str(num)
        n = len(s)
        dp = [1] * n
        for i in range(1, n):
            dp[i] = dp[i - 1]
            if 10 <= int(s[i - 1:i + 1]) <= 25:
                dp[i] += dp[i - 2]
        return dp[-1]

进而可以优化到空间 $O(1)$

class Solution:
    def translateNum(self, num: int) -> int:
        s = str(num)
        n = len(s)
        a = b = 1
        for i in range(1, n):
            if 10 <= int(s[i - 1:i + 1]) <= 25:
                temp = a
                a = b
                b = temp + b
            else:
                a = b
        return b

更多题解可以访问我的 LeetCode 题解仓库：https://github.com/azl397985856/leetcode 。 目前已经 30K star 啦。

大家也可以关注我的公众号《力扣加加》获取更多更新鲜的 LeetCode 题解